THE LAWS OF THE PHYSICAL WORLD

LET'S THINK ABOUT SOME DAILY EXPERIENCES TO EXPLAIN WITH SIMPLE WORDS AND SOME FORMULAE THE LAWS WRITTEN BY GOD IN THE STRUCTURE OF THE PHYSICAL WORLD

5

THE FRICTION

The forces of friction are resistant forces,acting against the motion or rolling of a body on the surface of another body which is in contact with.
The contact forces acting between the surfaces of two bodies are determined by the attractive electric forces by which the molecules interact each other.
If a body is at rest on a horizontal rigid surface,we observe that the least modulus of the horizontal force Fo _min we need to apply to the body to start its motion, is directly proportional to the modulus of the vertical force F_v that pushes the body against the surface.
F_v is given by the weight P , to which we have to add each possible additional vertical force Fa pressing the body against the surface:
Fo _min = m_s  Fv  = m_s ( P + Fa ), where m_s ( P + Fa ) is the static friction force F_fs.
The proportionality coefficient m_s (which is less than one) between the surfaces in contact is the static friction coefficient,that depends on the nature of the surfaces in contact and decreases if these are lubricated. As soon as the body starts to move, the coefficient m_s  is replaced with the dynamic friction coefficient m_d ,that is smaller than the static one. Therefore the force of dynamic friction F_fd acting between two bodies that are moving being in contact each other, is always smaller of the static friction force F_fs.
Example
If a block with a weight of 100 kg , placed on an horizontal surface, starts to move when the horizontal force applied to it assumes the value of 40 kg, the coefficient of static friction is m_s   = 40/100 = 0,4.
As soon as the intensity of the applied force overcomes the value of 40 kg, the block accelerates.
To make the body be moving with a constant speed, the applied force must be diminished shortly after starting, because now the force of static friction is replaced by the one of dynamic (or kinetic) friction.
If instead, we suppose that the dynamic friction coefficient is 0,25, the intensity of the horizontal force that has to be applied to maintain the block in an uniform motion is 0,25 * 100 = 25 kg.
The friction between two bodies moving in contact each other is the so-called sliding friction, and it is smaller than the rolling friction that takes place when a body rolls on another one.
For this reason in the machines the ball bearings, which are based on the rolling friction, are more advantageous than the ones founded on the lubricates surfaces.
The internal combustion engines need a continuous lubrication of the cylinders, by means of pressured oil, to avoid the seizure of pistons.
The gears of some mechanical devices, as the differential and the speed change device,operate immersed in oil to minimize the friction and so guarantee operation safety.
The presence of the friction forces, that dissipate mechanical energy into heat, isn't always undesirable:
- The friction clutch and the brakes of a car are based on sliding friction;
- We should not are able to walk neither run without the forces of friction between our shoes and the ground;
- A railway or road vehicle would not be able to move without the friction force, respectively among the wheels and the rails and among the tires and the road surface;
- A car or a motor-cycle, to be moving along a curve,need some friction centripetal forces that must be the greater, the greater is the speed and the smaller is the radius of the curve.

THE HYDRODYNAMICS RESISTANCE

A body moving in a liquid is liable to the resistant forces produced by the intern friction of the liquid, that is by the viscosity.
The viscosity of a liquid is produced by the attractive electric forces acting among the molecules, and it is decreasing with the increasing temperature of the liquid.
The fact that the viscosity of an oil decreases with the increasing temperature, explains the difficulty that happens in starting the engine of a car when the temperature is very low.
The intern friction of a liquid and the friction between this and the surface of a moving body, determine the hydrodynamic (or viscous) resistance to the motion, that is directly proportional to dimensions and speed of the body.
If the body is moving with a speed greater than 2 m/s, the resistance varies in terms of the square of the speed ( hydraulic resistance ).

THE AERODYNAMIC RESISTANCE

If a body is moving in a gas,it is subjected to a resistant force,that is the resistance to motion in the medium or the aerodynamic resistance, that depends on the square of the speed of the body, on the density of the gas, on the surface of the body, that is on the cross area of the surface projected by the body on a plane perpendicular to the direction of the speed, and on a form factor that varies in terms of the geometric characteristics (the aerodynamic profile) of the body.
Examples
In the case of a body with a great surface, for example a parachute, the aerodynamic resistance is so great that the fall speed stabilizes about a constant value, that is the smaller, the greater is the surface of the parachute.
Because the aerodynamic resistance R = Cr r V ² S is directly proportional to the area S of the parachute, to the density r of the air and to the square of the speed V , after some time the fall speed becomes constant according to the inertia principle.
Then the weight force P = Mg and the aerodynamic resistance
R = Cr r  V ² S are balancing each other, where Cr is a coefficient of proportionality that depends on the form of the body and it is analogous to the well known   coefficient Cx that determines the aerodynamic resistance acting on a car.
The constant speed V of the falling body is gotten by extracting the square root of the ratio [Mg/(Cr S r)].
The aerodynamic resistance is always directed along the perpendicular to the cross section of the moving body.
The aerodynamic resistance acting on the aileron of a F1 race-car or on the wings of an airplane, because the mobile surface is disposed sideways in comparison with  the direction of motion, it may decomposed in two components: the vertical component, in the case of the F1 race-car pushes it against the ground, increasing the adherence among the tires and the road surface; in the case of the airplane instead, it is up directed and constitutes the so-called carrying capacity (force) of the wings, that has to overcome the weight of the airplane so that it is able to take off.
The horizontal component acts against the motion in both cases, and consequently against the propulsive force.
In the case of a car, the aerodynamic resistance in relation to the cross-section of the car body, determines the maximal speed corresponding to the maximal power generated by the engine.
In fact, with the increasing speed, the aerodynamic resistance, added to the rolling resistance of the car, that is directly proportional to both the weight and the coefficient of rolling friction between the tires and the road surface, is balancing the propulsive force , till the acceleration is reduced to zero and the speed remains constant,according to the inertia principle.
If the cross-section of the car body is S = 1,5 m² , and we consider the air density r = 1,29 kg/m³, the maximal speed Vmax = 130 km/h ~= 36,11 m/s, the value  Cx = 0,2 , the weight P = 1000 kg  and the coefficient of rolling friction Cv = 0,01 , we get the following values:
Ra =(aerodynamic resistance) = Cx r S V ² = 0,2 x 1,29 x 1,5 x (36,11)² = 504, 62 N = (504,62/9,8) kg = 51,49 kg.
The resistance to the rolling is instead:
Rr = Cv P = 0, 01 x 1000 = 10 kg.
Therefore, at the maximal speed of 130 km/h the engine generates the maximal power Pmax, which is given by the product of the total resistant force:
Rt = Ra + Rv = 51,49 + 10 = 61,49 kg at the speed Vmax:
Pmax = Rt Vmax = 61,49 x 36,11 (kgm/s) = 2220,4/75 HP = 29, 6 HP
( 1 Hp = 75 kgm/s ).
The power that has to be generated to overcome the aerodynamic resistance is:
Pa = Ra Vmax = 51,49 x 36,11 ~= 1859,3 ~= 24,79 HP, while the power ncessary to overcome the resistance to the rolling is
Pv = RvVmax = 10 . 36,11 ~= 361,1 kgm/s ~= 4,814 HP.
The simulations by computer and the aerodynamic tests that are performed in the the wind tunnels of the car-factories, are requested to optimize the form of the car-body to make the engine generate the optimum power in relation to the maximal speed.

THE PASCAL PRINCIPLE

The Pascal principle (a French philosopher and mathematician , 1623- 1662) is fundamental to study the statics of  fluids ( liquids and gases ), that are characterized by a greatest mobility of the molecules, because the electric forces by which these interact each other, are much reduced in comparison with the ones acting inside crystals.
To enunciate the Pascal principle we need to remember the fundamental properties of fluids.
While a liquid has the minimal compressibility and assume the form of its container, with a constant volume, a gas instead is easily compressible and, because of the very weak attractive forces among the molecules (the Van Waals forces), that are moving with high thermal motion speeds, they are expanding till take the whole volume of the container, acting a pressure on the walls of it.
How can be defined the pressure of a fluid?
It is the force acting along the perpendicular to any unitary surface that is in contact with it, and it is measured by the force per surface unit:
1) N/m² = Pa (Newton/meters²) = Pascal;
2) kg/cm² ~= 9,81 N/cm² = 98100 N/m² = 98100 Pa;
3) atmosphere = 1,033 kg/cm².
Since the pressure is definite by the relationship p = F/S between the force F acting along the perpendicular to a surface and the area S of it, if we know the value of the pressure in an assigned point of the liquid, we may calculate the force F = pS acting along the perpendicular to the surface S.
If in fact we consider a tank containing a liquid in the equilibrium condition (that is when its free surface is horizontal), the pressure forces the liquid acts on all the tank walls, produces, according to the III law of dynamics, some pressure forces that are equal and acting in opposite directions with respect to the ones the tank walls effect on the liquid.
These reaction forces, if weren't directed along the perpendicular to the tank walls, would make the liquid flow parallelly to them, because of the great molecular mobility.
Therefore it is deduced that in a fluid the pressure forces act always along the perpendicular to the tank walls and to any surface placed inside the fluid, independently from the orientation of the surface.
The pressure of the gas in a container is the effect of the continuous collisions of the molecules against the walls, and increases with the increasing temperature,because the molecular kinetic energy is directly proportional to the absolute temperature ( in Kelvin degrees ) of the gas.
The electric forces acting among the high mobility molecules of a fluid make it possible that the pressure we act in any point of its mass,is transmitted along every direction and with the same value to whole the fluid mass, without any diminution.
Therefore the Pascal principle states that, if a fluid is inside a container and the pressure value at any point of it is increased, this increase of pressure is transmitted unchanged to whole the fluid and to the walls of the container.
Examples
If a liquid fills a cylinder furnished with a piston effecting a pressure on the liquid, pushing down of the piston determines a pressure increase that is transmitted unchanged to whole the liquid and to the walls of the cylinder.
An important application of this principle concerns the braking system of a car, that permits to apply to the front and rear brakes the force acted by the foot of the driver, across a pressured liquid that transmits the pressure increase.
We remember besides that on the Pascal principle is based the operation of the oil-pressured systems used in excavators, bulldozer and so on, and the operation of hydraulic presses, that apply to a mechanical piece that has to be moulded, forces of several tons by means of much more little engine forces.

OIL PRESS

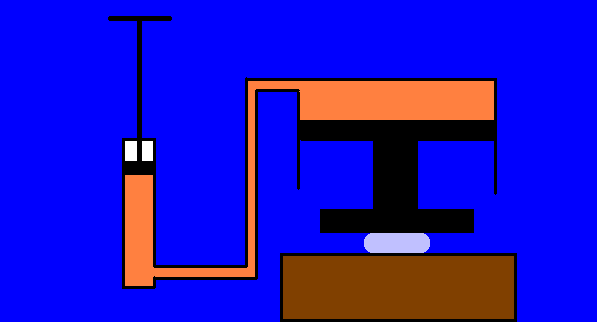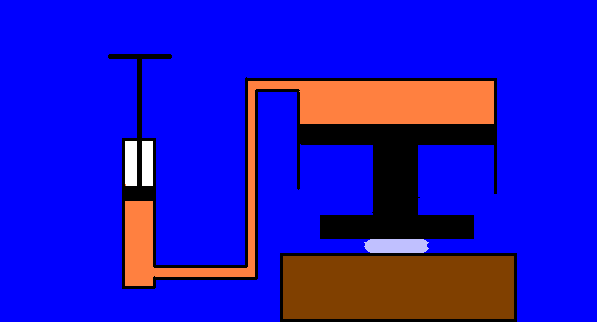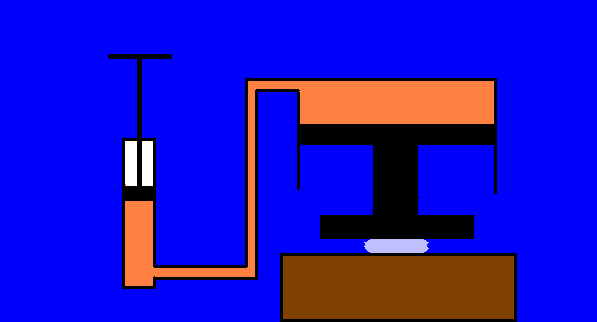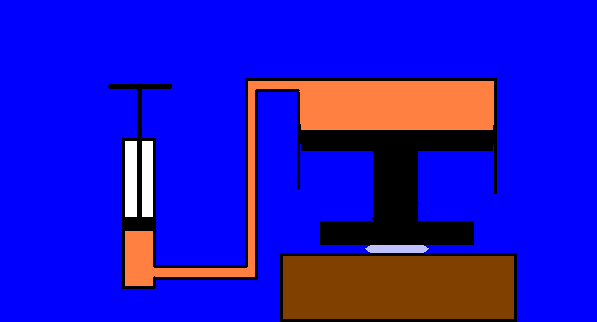
In an oil-filled cylinder a piston with a surface of 10 cm² is pushed down of 100 cm,under the action of a force of 10 kg, transmitting a pressure increase of 10 kg/10 cm² = 1 kg/cm² to another piston with a surface of 1 m² = 10000 cm².
On the great piston is acting a force of 10 tons (10000/10 = 1000 times greater than 10 kg), whereas its displacement is 1000 times smaller ( 1 mm ) than the one of the little piston.
The work made on the little piston is L = 10 kg x 1 meter = 10 kgm  (kilogram.meters),and it is about equal to the work made by the great piston on the object that has to be moulded (this is the principle of operation of the hydraulic press ), provided it is negligible the work that is transformed into heat because of the friction forces and the viscosity of oil.

ARCHIMEDES AND STEVINO'S PRINCIPLES

The principle of Archimedes is a direct consequence of the fact that the hydrostatic pressure a liquid produces because of the gravity force, depends on both the density and the height of the liquid inside a container.
If we consider in fact a liquid which is in static equilibrium in a container, the hydrostatic pressure p at any point of the liquid at a depth h under the free surface of the liquid, is given by the formula:
p = p_o + r g h ( this is the principle of Stevino), in which r is the density of the liquid, g is the gravity acceleration and p_o is the atmospheric pressure acting on the free surface of  the liquid.
The product r g h is the weight of a liquid column with the density r , the base of 1 cm² and the height h, and is numerically equivalent to the hydrostatic pressure, that depends only on the depth h under the free surface of the liquid and produces always forces (pressure forces) directed along the perpendicular to the surface that is considered.
The Archimedes principle states that a body immersed in a liquid or in a gas with the density r , is subjected to the force S , the so-called hydrostatic thrust, which is equal to the weight of the liquid volume V removed by the body.
If the body is partially immersed in the liquid,(if the body floats in the liquid), the hydrostatic thrust equates the weight of the volume of the body part immersed in the liquid.
The Archimedes thrust S = r gV is generated by the resultant of all the forces the fluid produces on the surface of the body by means of the hydrostatic or aerostatic pressure.
In gravity absence conditions, for example in a spaceship orbiting around a planet or a satellite, there is no hydrostatic pressure and then there is no thrust of Archimedes.
A body immersed in a liquid floats if the Archimedes thrust overcomes its weight.
In this case the resultant of the hydrostatic forces pushes the body toward the liquid free surface, till the thrust produced by the immersed part doesn't equate the weight of the body.
Ships, submarine, hot-air balloons and dirigibles operate according to the Archimedes principle.
A submarine,pumping some water into or out its watertight compartments, is able to control the difference,up or down directed, between the resultant of the hydrostatic pressure forces and its weight, respectively when it is going up again to the sea surface or when it is submerging.
When the weight of the submarine equates the resultant of the hydrostatic pressure forces, once it has reached the pre-established depth, can remain at this constant depth.
An hot-air balloon is subjected to an ascensional force Fa which is given by the difference between the aerostatic thrust S and the weight P:
Fa = S-P = r_cVg- r_hVg, where r_c and r_h are, respectively, the density of the external cool air and the one of the hot air inside the ballon.

THE MASS CONSERVATION PRINCIPLE

The mass conservation principle,formulated in 1789 by the French chemist Lavoisier and already expressed by Lucretius in the poem "De rerum natura", states that the whole amount of matter in Nature is constant and indestructible.
Therefore, in any system and, by extension, in the universe,the total amount of matter is always the same.
The matter is subjected to physical or chemical transformations, but it is never destroied.
In Nature nothing is destroying, everything is transforming .
Example
The combustion of coal (C) or methane (CH₄) is a chemical reaction between carbon and oxygene or between methane and oxygen.
The combustion products of the chemical reaction consist, in the case of coal,of carbon monoxide (CO) and carbon dioxide (CO₂);
instead,in the case of methane,they consist of carbon dioxide and steam
( CH₄ + 2 O₂ = CO₂ + 2H₂ O ).
If we weighted the fuel ( coal or methane ) , the oxygene and the combustion gases, we could verify that the total mass of the reaction products is always equal to the total mass of the reagents, provided we neglect, in the first approximation, the extremely little mass of the reagents that is transformed into heat according to the relativistic equivalence principle between mass and energy.

PREVIOUS   PAGE

NEXT   PAGE