

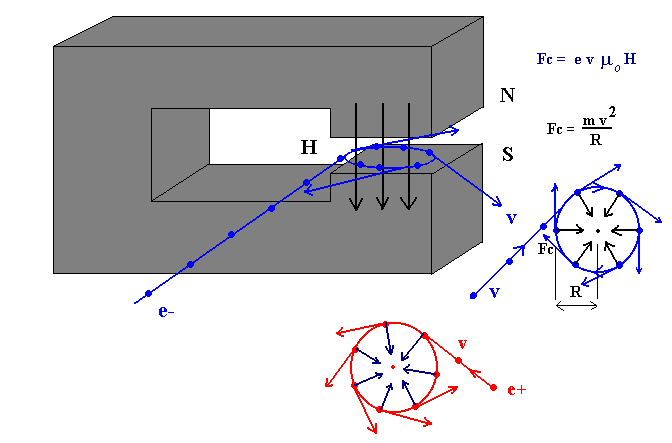
An electric charge, moving with the speed v in a magnetic
field having the intensity H, is subjected to the Lorentz
force, which acts along the perpendicular to the plane individuated by the lines of force
of the magnetic field and by the motion line of the charge (the instant
direction of its speed ), with an intensity given by the formula:
F = kqvH, where k is a constant
of proportionality depending on the medium which the charge is moving inside, and on the
measure unit system which is used (for example, in the international system M.K.S.A. and
in vacuum, practically also in the air,k coincides with the
so-called vacuum magnetic permeability mo
= 4 p 10-7 Henry/meter ).
The force of Lorentz acts on both the electrons moving inside the electric circuits (the
electrons constituting the electric current) and on any charged particle moving in the air
or in vacuum.
If a charged particle is moving with a velocity perpendicular to the lines of force of the
magnetic field, the force of Lorentz constitutes the centripetal force that is continously
diverting the particle from its instant motion line, in such a mode that its trajectory is
a circumference placed in a plane perpendicular to the lines of force of the magnetic
field.
Instead, if a charged particle is moving along a direction which is oblique with respect
to the lines of force of the magnetic field, the component of its velocity along the
perpendicular to the magnetic field direction, determines the intensity of the Lorentz
force, while the component of its velocity along the magnetic field direction,makes the
plane of the circular trajectory be shifting with a constant speed parallel to itself .
Therefore, as a consequence of the Galilean principle of the motion composition, the
charged particle describes an helical (spiral) motion having its axis along the magnetic
field direction.
Some examples:
The flux of the particles constituting the solar wind (high energy protons and electrons)
interacts with the Earth magnetic field that, by means of Lorentz's force, makes them
describe spiral trajectories along the lines of force directed from the magnetic North
pole toward the South one.
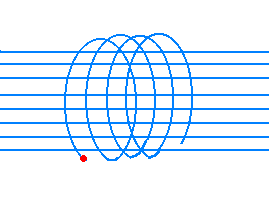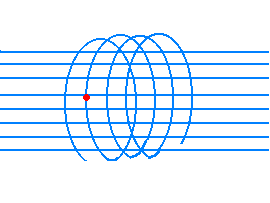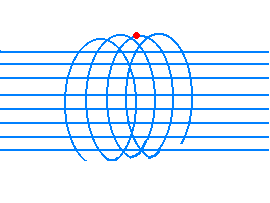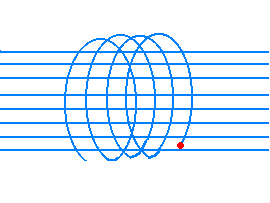
Therefore electrons and protons are trapped by the Earth magnetic field giving rise to
two radioactive zones (the Van Allen zones), that were discovered in 1958 by means of the
first USA artificial satellite of the "Explorer" series.
The Van Allen zones give rise to a natural biological screen that attenuates strongly the
flux of the solar ionizing particles investing the terrestrial surface.
The interaction of the particles of the solar wind with the terrestrial magnetic field
is accountable for the polar auroras that are observed in coincidence with notable
periodical increases of the solar activity (sunspots and magnetic storms ).
In the circular accelerators for elementary particles ( cyclotrons, electro-synchrotrons,
proto-synchrotrons and storage rings ), the force of Lorentz produced by the interaction
of the charged particles with intense magnetic fields, determines the radius R of the circular trajectory and then the dimensions of the
accelerator,which depends, with an assigned speed v, on the
mass m, on the electric charge q
of particles and on the intensity H of the magnetic
field:
(centripetal force = mv2/R ) = ( the force of
Lorentz = kqvH);
R = mv/(kqH), where k is the
proportionality constant of the Lorentz law .
Therefore are necessary very strong magnetic fields, produced by superconducting magnets
maintained at very low temperatures (a few Kelvin degrees) to reduce the dimensions and
the cost of the accelerators, compatibly with the very high energy ( 1000 Gev ) that must
be reached.
The circular accelerators operating at the CERN of Geneva and at the FERMILAB of Chicago
have circumferences of several kilometers .
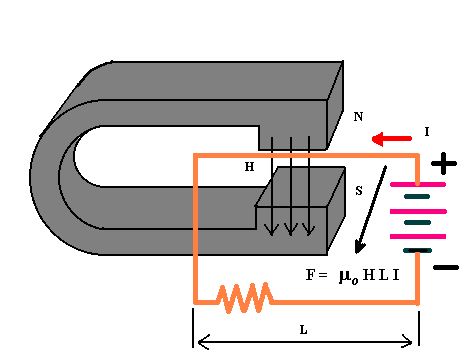
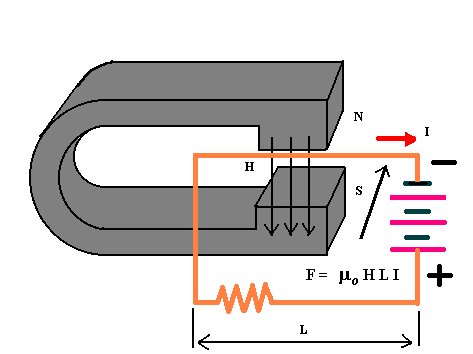
The force of Lorentz that acts on the electrons constituting the electric current in a
conducting wire, determines the macroscopic force acting on the conductor when it is
placed in a magnetic field.
The magnetic force F = k H L I is directed perpendicularly to
the plane individuated by the wire and by the direction of the magnetic field, and its
intensity is directly proportional to the current intensity I,
to the length L of the wire and to the intensity H of the magnetic field ( k is the
proportionality constant of the Lorentz formula).
The transformation of electric power into mechanical energy in an electric motor is
possible as a consequence of the fact that the electromagnetic forces acting on the
conducting wires of the rotor winding by means of the magnetic field produced by the
stator, produce a system of torques, that are adding each other to give the engine torque
generated by the electric motor.
Even the macroscopic electrodynamic forces acting among the conductors of an electric
circuit (for example among the coils of the winding of an electromagnet, an electric
motor, a dynamo, an alternator or a transformer) are owing to the microscopic Lorentz
forces to which are subjected the conduction electrons.
That forces can be always reduced to a force and a torque, which are described by Ampere's
electrodynamics laws .
In the particularly simple case of two rectilinear and parallel conducting wires of length
L, in which are flowing the currents with the intensities I1 and I2,
placed in vacuum (practically also in the air ) at the distance d,
the electrodynamic force acting between them is directly proportional to the product of
the current intensities I1 and I2 and to the length L, and
is inversely proportional to the distance d:
F = k I1I2L/(2pd),
where k is the proportionality constant of Lorentz's
law.
If, in particular, in both the conducting wires flows the same current (coils of a winding
), electrodynamics forces depend on the square of the current intensity.
The Ampere law of the magnetic concatenation was generalized by Maxwell, who,
exclusively on the base of physical-mathematical elaborations, deduced that a varying
magnetic field may be produced, besides by a current flowing in an electric circuit, even
by a varying electric field in vacuum, even if there are neither electric charges nor
electric circuits.
For analogy with the magnetic field generated by electric charges moving in vacuum and by
electric circuits, Maxwell introduced the so-called "displacement currents" in
dielectric (insulating) materials, that are produced by varying electric fields.
Therefore, as exist magnetic lines of force concatenated to an electric circuit, so exist
magnetic lines of force concatenated to a varying electric field.
Maxwell, on the basis of the fundamental principles that govern the electric and magnetic
phenomena (the Coulomb's, Ampere's and Faraday-Neumann's laws), succeeded to elaborate his
theory of electromagnetic phenomena, furnishing a genial and elegant unitary
representation of both electric and magnetic phenomena, by means of four fundamental
equations (Maxwell's equations ), that can be expressed both in a differential form
relating to infinitesimal spatial zones in which take place electromagnetic phenomena, and
also in an integral form, more comprehensible and suitable to describe the electromagnetic
phenomena that are observed in laboratory.
The first equation, equivalent to the Gauss theorem, can be obtained on the basis of
Coulomb's law, and it expresses that the flux of the electric field (number of the
lines of force of the electric field ) coming out of a closed surface containing one
or several electric charges, is directly proportional to the algebraic sum of all the
positive electric and negative charges, which are placed at rest in assigned points of the
space inside the considered surface.
For example, if we consider a spherical or a cylindrical surface containing some electric
charges , it is possible, by the first Maxwell's equatio, to calculate the intensity of
the electrostatic field in the points of the space inside and outside the considered
surface.
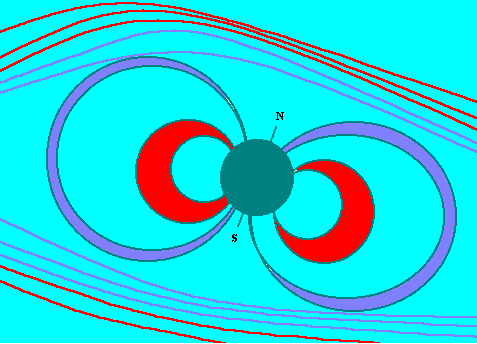
The second Maxwell's equation is relating to the characteristic property of the magnetic
field, whose lines of force are always closed, since don't exist any single magnetic poles
.
Therefore, if we consider a closed surface in which are placed some magnets or electric
circuits, the number of the magnetic lines of force coming out of the surface is
always equal to the number of the ones going into the surface, since the lines of force
that have origin inside the surface go back always into it ending in the same points from
which they originated.
The third Maxwell's equation corresponds to the electromagnetic induction law
(Fraday-Neumann's law), that implicates always the existence of a varying electric field
along a closed line (an electric circuit or a closed line traced in vacuum) crossed by the
lines of force of a time changing magnetic field.
The fourth Maxwell's equation corresponds to the generalization of Ampere's law to
the the magnetic fields generated both by electric charges moving in vacuum, inside
liquids, gases and conductors (that is by electric currents ), and also by
"displacement currents", that is by time changing electric fields.
Therefore there is always a magnetic field concatenated to a closed line, inside matter or
in vacuum, which is crossed by moving electric charges (electric currents) or by the lines
of force of a time changing electric field.
The most important result of Maxwell's electromagnetic theory consists in the fact that
the fourth equation of the electromagnetic field implicates the existence of
electromagnetic waves that are propagating in vacuum with a speed that equalizes the speed
of light
(300000 Km/s ), transporting energy and momentum of electromagnetic kind.
As a consequence of this result Maxwell enunciated the electromagnetic nature of all the
luminous phenomena (the so-called electromagnetic theory of light).
Her intuition was brightly confirmed in the ending period of XIX century by means of the
bright experiments effected by Hertz on the electromagnetic waves ( Hertzian waves ).
Hertz succeeded to produce by electromagnetic waves reflection, refraction, interference,
diffraction and polarization phenomena analogous to the ones produced by the luminous
waves.