

Ohm discovered the fundamental law of the electric circuits by analogy with the
phenomenon of the propagation of the heat by conduction.
As the heat flux Q/t = KS (T1-T2)/L (calories/second)
goes across a layer of a conducting material with the lenght L,
between whose sides, having the section S,exists a given
difference of temperature T1-T2 , with T1>T2 , so the electric current intensity I = Q/t (that is the ratio electric charge/second) that goes across
a conducting wire, with the lenght L and the section S, is directly proportional to the potential difference V1-V2 applied to the extremes of the wire:
I = k S (V1 - V2)/L, where k is a constant (the so-called specific conductivity), depending on
the conducting material.
The electric current I is directed, by convention, as the
thermal one, from the points at a greater potential (V1)
toward the ones at a lower potential (V2).
In fact, although is still operating this convention, established before the discovery of
electron, however we know that the effective direction of the current in an electric
conductor is the same as the one of electrons, that,by means of their negative electric
charge,are moving from the points at a lower potential toward the ones at a greater
potential.
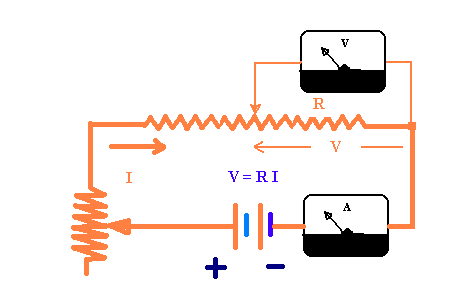
If we rewrite Ohm's law as V1 - V2 = I
[L/(Sk)] = I R, the constant
R = L/(Sk), called resistance, evidences the direct
proportionality between I and V1
- V2 , and is directly proportional to the lenght L
of the conducting wire ed inversely proportional to its section S.
When electric current flows in a conductor,a work is made by the electric field
accelerating the charges constituting the current.
This work, because of the resistance R, is transforming into
heat according to the Joule effect.
In fact, one of the several methods used to determine experimentally the mechanichal
equivalent of heat (that is the number of joules corresponding to one calory) or the
thermal equivalent of work (that is the number of calories corresponding to one joule) is
based on measuring by a voltmeter, an ammeter and a chronometer the electric energy W = V I t = R I t = V2 t/R (these are the formulae of
the Joule effect) that is transforming into heat in a resistor R
within the time t, and on measuring also, at the same time,
by means of a calorimeter,in terms of the thermal increase (T2-T1)
of an assigned mass (M) of the calorimeter liquid (water or
mineral oil), with the specific heat c (expressed in
calories/gram °C), the heat Q = M c(T2-T1)
generated by the resistor R as a consequence of the Joule
effect.
The ratio between these measures gives the equivalence ratio between joules and calories:
4,18 Joules/calory or 0,24 calories/joule.
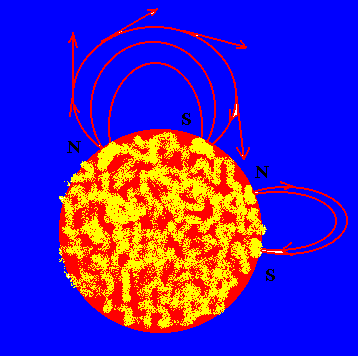
Already in the ancient Greece (VI century b.C.) was known the property of the magnetite
(an iron ore, ferrous-ferric oxide, mined for the first time near the town of Magnesia),
of attracting iron filings , behaving as a natural magnet.
The compass, whose invention is attributed to Chinese,and that was imported in the western
world about to the XII century, furnishes a clear example of the action of the terrestrial
magnetic field on a magnetic needle.
A magnetic needle is a thinnest steel rod which has been magnetized by approaching a
magnetite piece, and is hinged so that it is able to rotate without friction in an
horizontal plane, till reach, after an oscillation series, an equilibrium position that
indicates the direction of the Earth magnetic field.
Taking account that the Earth behaves as a magnet whose axis forms with the polar axis an
angle of about 11°,and that crosses the Earth surface in two points, the magnetic Poles
North and South, near to the respective geographic poles,by convention we denominate as
North pole of the needle the pole directing toward the North magnetic pole in the
equilibrium position, while the South pole of the needle is the one directing toward the
South magnetic Pole.
A magnetic needle is a sensitive detector of magnetic fields.
We remember in this regard the experiences effected by the Danish physicist Oersted, that
in 1820 discovered that an electric circuit in which flows the continuous electric current
generated by a battery ,if it is placed in proximity of a magnetic needle, makes it swerve
from its position of equilibrium in the Earth magnetic field.
Since the same effect is observed if to the magnetic needle is approached a magnet,it
is deduced that an electric circuit produces in the surrounding space a magnetic field,
and it is therefore equivalent to a magnet, as it was shown by the French physicist Ampere
(Ampere equivalence theorem) not long after the discovery made by Oersted.
To visualize the force lines of a magnetic field it is enough to use some iron filings.
If a magnet is placed, indeed, under a sheet of cardboard on which have been distributed
some iron filings, these are disposing along many curvilinear segments,the so-called lines
of force of the magnetic field, that are thickened in correspondence of the extremity (the
poles) of the magnet ;so it is gotten a magnetic spectrum, that visualizes how the
magnetic field varies in the space surrounding the magnet.
In an analogous mode can be visualized the magnetic lines of force associated to any
electric circuit: a rectilinear circuit, a conducting turn or an helix
winding (the so-called solenoid) consisting of many conducting turns
connected in series, in which flows the same current.
The substantial difference between the lines of force of the magnetic field and the ones
of the electric field consists in the fact that the magnetic lines of force are always
closed, because they have neither beginning nor end, as shows the classical experience of
the broken magnet.
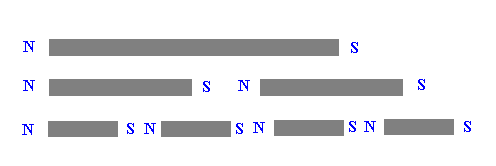
Breaking in more pieces a magnet,it is impossible to separate the north pole from the
south one,differently from what happens with the electric charges, because single
magnetic poles don't exist.
In the case of the electric field, instead, the lines of force of the field produced by a
pointlike charge,are directed, by convention, along the radii coming out from the charge,
if it is positive, going toward the charge, if it is negative.
As we said, the spectrum produced by each of the aforesaid circuits can be gotten by
disposing some iron filings on a sheet of cardboard crossed by the conductor wire or the
conducting turns.
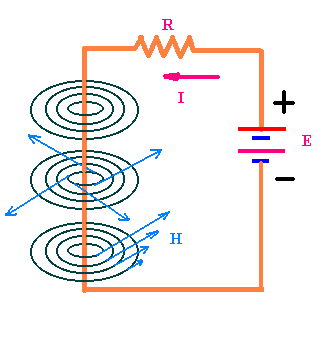
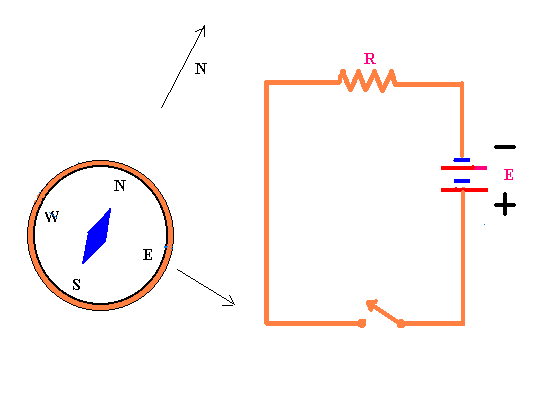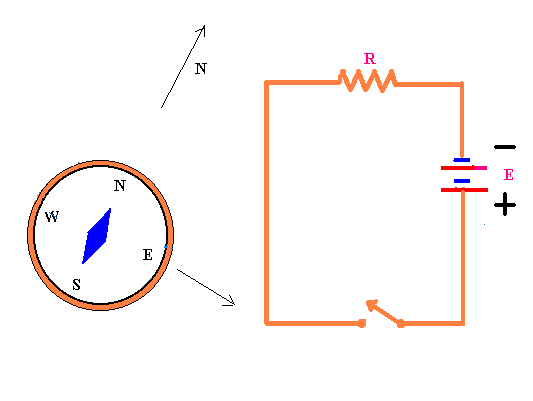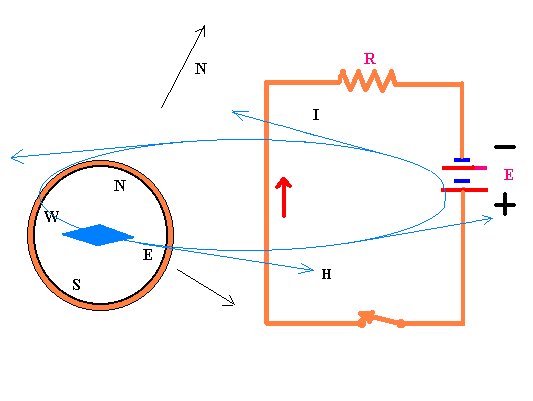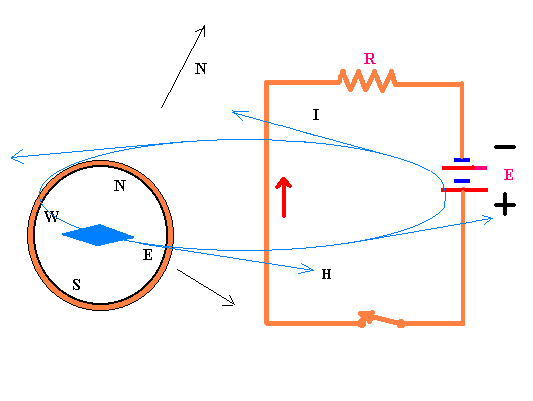
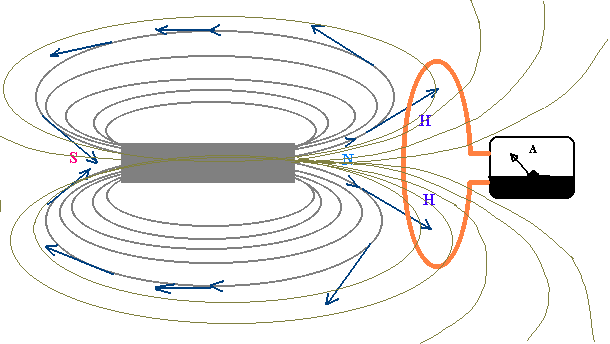
In particular,the intensity H (expressed in
ampere-turns/meter, At/m) of the magnetic field produced by the electric current I flowing in a rectilinear wire much long in comparison with the
distance between it and the point where is measured the magnetic field, is directly
proportional to the current intensity ( in ampere ) and inversely proportional to
the distance d (in meters) from the wire: H = k I/d
(this is the law of Biot and Savart ),
where k = 0,1592 ampere.turns/ampere is a constant of
proportionality that depends on the system of measure units.
In this case the lines of force of the magnetic field are the concentric circumferences
with the center on the wire and they are placed in a plane which is perpendicular to it.
In the case of a circular coil with the radius R (in meters),
the magnetic field at the center of the coil is directed along the perpendicular to the
its plane , and its intensity H (in Asp/m ) is directly
proportional to the current intensity I (ampere) and
inversely proportional to the radius R :
H = k I/R , where k = 0, 5 ampere.turns/ampere.
In the case of a rectilinear solenoid consisting of n coils
with a radius much smaller than its length L, in which flows
the current intensity I, the magnetic field H is directed along the axis of the solenoid and its intensity H (in Asp/m) is given by H = n I/L.
The magnetic field generated by the solenoid is uniform, since it has a constant
value inside it, and its lines of force are parallel to the axis of symmetry.
The aforesaid formulae derive from the application of Ampere's law, which is known also
as the theorem of the magnetic concatenation, that states that an electric circuit
generates a magnetic field whose lines of force are closed lines, such that, if we
calculate the sum of all the infinitesimal elementary products, of the type Hi dli, where dli is a infinitesimal
displacement tangent to the line of force and Hi is the
relative value of the intensity of the magnetic field, when we make the number of such
products become infinite, we get a value that is equal to the current intensity flowing in
the circuit.
If, in particular cases, the magnetic lines of force underline a symmetry with respect to
the circuit, as it happens in the simple case of the rectilinear wire that produces the
magnetic field H = k I/R, whose lines of force are concentric
circumferences with the radius R, it is gotten:
H 2p R = I ; H = I/( 2p
R) = 0,1592 I/R.
Both the macroscopic magnetic fields, that are produced by electric circuits and permanent
magnets, and the microscopic ones, that are associated to the orbital motions of electrons
in atoms and to the intrinsic angular momentum of subatomic particles (spin), are
always produced by electric charges moving in comparison with the observer that measures
the field, and then, by macroscopic or microscopic electric currents, respectively.
The hypothesis that also the field of the permanent magnets is generated by microscopic
currents, formulated by Ampere, was brightly confirmed by the discovery of electron spin
and of the associated elementary magnetic moment (the so-called Bohr's magneton).
Examples:
1)the electron beam that produces the image on the screen of a television set or of a
monitor, produces a magnetic field which is like that the one produced by a rectilinear
wire in which flows electric current.
2) A circular beam of charged particles (electrons, mesons, protons, ions ) that revolve
with a speed near to that of light in a synchrotron (a circular accelerator for elementary
particles ) generates a magnetic field which is like the one produced by a coil coinciding
with the circular trajectory that the particles follow for effect of the strong magnetic
field acting along the perpendicular to the circular beam.
In 1831 Michel Faraday discovered that any electric circuit , even if it has no
electric generators (dynamos ,alternators, power supplies, batteries) and consists only of
passive components ( resistors, solenoids and capacitors, that absorb electric energy ),
generates an induced electric tension when it is crossed by the lines of force of a
varying magnetic field.
In short this law states that, when the magnetic flux linked to an electric circuit, is
time varying, is generated a tension by electromagnetic induction, as if inside the
circuit were inserted an electric generator whose tension is directly proportional to the
variation of the number of the magnetic lines of force per a time unit.
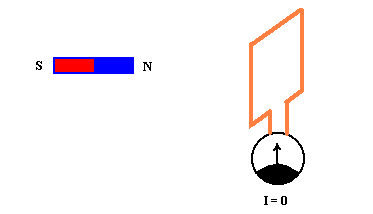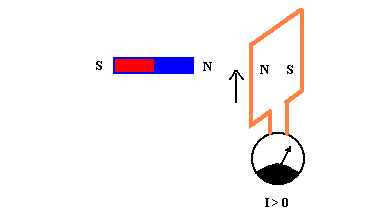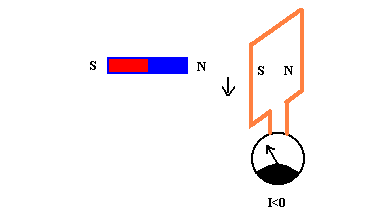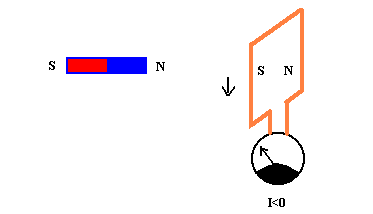
The temporal variation of the magnetic flux linked to the circuit may be verified by
several methods:
1) moving a permanent magnet, an electromagnet or another electric inductor circuit with
respect to the induced electric circuit (that is subjected to electromagnetic induction).
In this case the magnetic lines of force are cut by the circuit.
2) maintaining at rest the permanent magnet, the electromagnet or the inductor electric
circuit with respect to the induced electric circuit and deforming the contour of this, in
such a mode to determine a variation of the section crossed by the magnetic lines of
force.
3) maintaining at rest the permanent magnet, the electromagnet or the inductor electric
circuit with respect to the induced electric circuit and approaching or leaving in
proximity of the induced circuit pieces of ferromagnetic materials (iron, steel, cobalt,
nickel,ferromagnetic alloys as Al-Ni-Co), that is materials having a great magnetic
permeability, capable of intensify, by magnetization, the existing magnetic field.
4) varying by a resistor (rheostat) or in any other mode, the current intensity in the
electromagnet or in the inductive electric circuit, maintaining at rest the induced
electric circuit.
5) Opening or closing the circuit of the electromagnet or the inductor electric circuit.
Analysing the experimental data provided by such apparently much different physical
phenomena, Neumann was able to derive the law of electromagnetic induction by the formula:
E =-DF/Dt,
where E is the induced electric tension, DF is the variation of the magnetic flux linked to
the induced electric circuit, and Dt is the time of the variation.
How much more rapid is the variation of the magnetic flux, as greater is the induced
electric tension.
So are explained all the observed phenomena, independently from the fact that the
variation of the magnetic flux is gotten by the relative motion between the magnet, the
electromagnet or the inductor electric circuit and the induced electric circuit, or in the
other ways.
If the induced circuit is open, between the extremes of it, provided the magnetic flux
varies with the time, may be measured the value of the induced tension, while there is no
current, because the circuit is open.
If instead the induced circuit is closed, it is generated the induced current I = E/R, that is gotten by applying Ohm's law, that is dividing the
value of the induced tension E by the ohmic resistance R of the circuit.
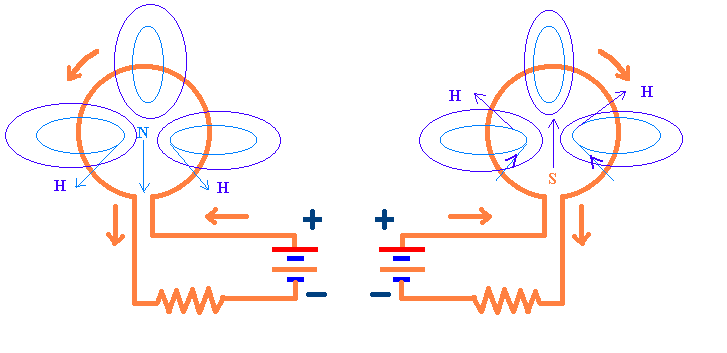
The minus sign was introduced by Lenz to express the experimental fact that the induced
current has always such a direction that it is opposing to the cause that generated it.
For example, if the induced current is caused by the approach of a magnet or of an
inductor circuit to the induced circuit, the induced current flows in such a direction
that is generated a magnetic field that rejects the inductive circuit.