

The heat energy may be transmitted from a body to another by conduction,convection,or irradiation.
We know that when two bodies at different temperatures come into direct contact, in
each point of their contact surface heat s from the body at a greater temperature to the
one at a smaller temperature, till is reached the thermal equilibrium condition, that is
till in all the points of both the bodies there is the same temperature.
The thermal equilibrium corresponds to equal amplitudes of the harmonic oscillations and
then to equal thermal agitation energies of all the atoms of both the bodies.
If instead between two bodies are placed one or several layers of other materials, the
heat transfer between the bodies happens indirectly, by means of the atomic harmonic
oscillations of the mediate materials.
The law that allows to calculate the heat quantity DQ that flows in the time interval Dt across a layer of material with
thickness Dx and
area S,between whose faces exists a temperature difference DT, it may expressed by
the relation
DQ =-(kSDT/Dx)
Dt, where k is a constant of proportionality, the so-called thermal
conductivity of the material.
For copper (good thermal conductor)
k = 0, 92 (calories/second)/[(cm2)(°C/cm ) ];
for cement (bad thermal conductor)
k = 0, 002 (calories/second)/[(cm2)(°C/cm )].
Therefore the Ith intensity of the heat flux
(expressed in calories/second ) across the layer is given by:
Ith = DQ/Dt
=-kS (DT/Dx).
The incremental ratio DT/Dx is the thermal
gradient ( from the Latin gradus, that is step),because it is the variation of
temperature between the sides of a layer with an unitary thickness.
The minus sign has been introduced to compensate the negative sign of the variation
(diminution) of the temperature DT in the direction of the heat flux,from the points at a greater
temperature to the ones at a smaller temperature.
Metals are the best thermal conductors, by means of free electrons, whose thermal
agitation energy is added to the one of the atoms in the crystalline structure.
Gases have values of the thermal conductivity from about 10000 to 100000 times smaller in
comparison with metals.
Example: The thermal flux across a plate of copper with the surface
S = 1 m2 = 10000 cm2 and thickness Dx = 2 cm, among whose
sides there is a temperature difference DT =-50 °C, is :
Ith = DQ/Dt
=-kS (DT/Dx) =-0, 92x10000x (-50/2) = 230000 calories/second.
If it is considered instead a plate of cement with the same surface and the same
thickness, the thermal flux is reduced to
Ith = DQ/Dt
=-kS (DT/Dx) =-0, 002x10000x (-50/2) = 500 calories/second.
The propagation of heat by convection takes place by the convective motions ( from the
Latin convehere = to transport ) of a fluid from the zones at a higher
temperature toward the ones at a lower temperature; the phenomenon consists in fact in
transferring heat from the warm zones to the less warm ones, by displacements of matter.
As a simple example of the heat propagation by convection,we consider the heating of the
water contained in a pot placed on a stove.
The warm water on the bottom of the pot is subjected to a density diminution and
,according to the principle of Archimedes, goes up, transmitting heat to the cool water
layers at the top of the pot; subsequently, because of the increasing density determined
by the heat transferred, the cooled water layers go back along the wall of the pot to the
bottom to be subjected to another cycle of heating-cooling-
heating.
In such a mode, by means of the continuous convective motions, heat propagates to the
whole water contained in the pot.
Winds and sea streams are generated by the convective motions, respectively, of the air
and water, because of the differences of temperature produced by the absorption of the
solar radiation.
In the case of the winds, on the warm zones of the Earth are formed some low pressure
areas (cyclonic areas ), toward which is directed the cool air coming from the
anticyclonic zones ( with a greater pressure ).
Sea streams are determined by the salinity and temperature differences among the water
layers placed at different depths.
On the convective motions is founded the operation of the domestic central heating system
that use the radiators: water circulates in pipes by the natural convective motions
generated by means of a boiler.
On the convective motions depend both the operation of all the thermal radiators used to
cool the heat engines, and also the operation of refrigerators (thermal condensers) and
electronic equipments.
In these devices the heat flux transferrd to the environment by the natural convection is
directly proportional to both the radiant surface and the temperature difference between
the radiator surface and the environment.
All the bodies with a temperature greater then the absolute zero
T = 0 °K (Kelvin degrees) or t
=-273,16 °C (Celsius degrees) irradiate energy by electromagnetic waves ( radiant
energy) with wavelengths distributed with continuity in the wavelenght band ranging from
the far infrared radiation to the visible one.
In fact, as Larmor showed, an accelerated electric charge emits energy
by electromagnetic waves; then thermal radiation is emitted because of the acceleration of
the oscillating atomic and molecular electric charges.
This happens as a consequence of the thermal oscillations of the atomic and molecular
electric charges.
It can be verified that the radiant power emitted by an unitary surface (the so-called
total emission), with reference to all the measurable wavelengthes, is given by the Stefan
law: E(watt/m2) = e s T 4,
where e (<1) is a coefficient that depends on the surface,
s =0,567
. 10-8 W/(m2K°4) is the Stefan-Boltzmann constant and T is the absolute temperature (°K).
If e=1, the radiant body is an ideal emitter ( black body ) ,which has the maximum
emission power.
If t= 1000 °C, T= 1000 + 273,16
= 1273,16 °K,
E=1 x 5,7 10-8 (1273,16)4= 149763,78
W/m2.
The energy conservation principle is, together with the fundamental conservation
principles of both the linear and angular momentum, a fundamental law of Nature, verified
universally as in the macroscopic physical world as in the microcosm.
It is an unifying principle that ties all the physical phenomena and furnishes an unitary
and integrated vision of all the physical theories, from the celestial mechanics to the
quantum mechanics,from the quantum theory of the fields to the standard model.
The enunciation of this principle goes up again to the XIX century, and contributed to its
discovery several researchers, some of which don't work as physicists:
Julius Robert Mayer (a German physician, 1814-1878 ),
James Prescott Joules (an English industrialist, 1818-1889 ),
Hermann Helmholtz [von] (a German physiologist, 1821-1894 ).
This researchers, independently from each other, contributed by different ways to
understanding this fundamental natural law:
Mayer by observations relating to the human physiology;
Joule performing with several methods the measure of the mechanical equivalent of the heat
(He determined that a little calory, that is the quantity of heat that has to be furnished
to the mass of one gram of water gram to increase the temperature of 1°C,is equivalent to
a mechanical energy of about 4,18 joule );
Helmholtz (1847 ) that understood for the first time that all the energy forms (
kinetic,potential, electric, thermal, chemical ) are equivalent.
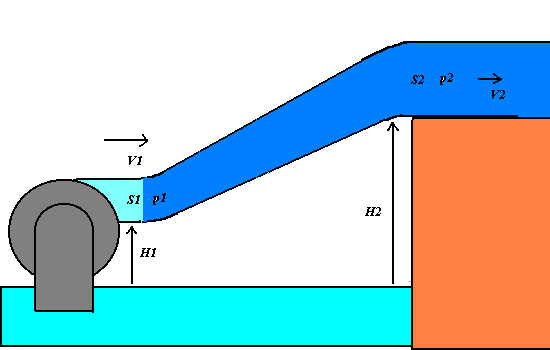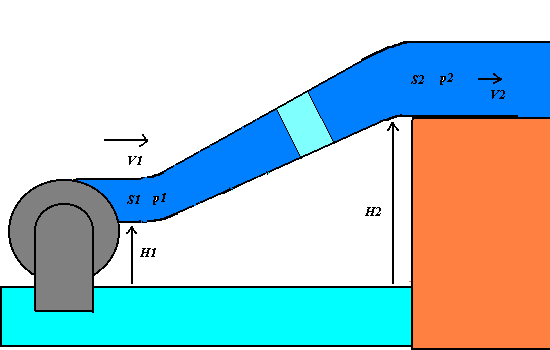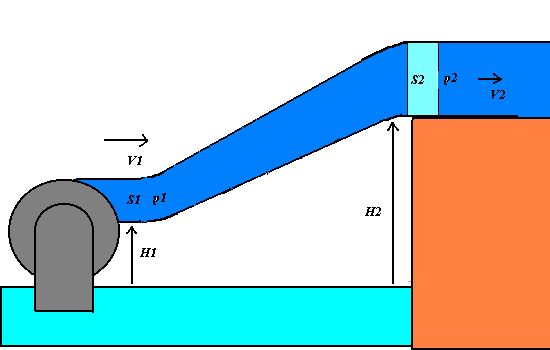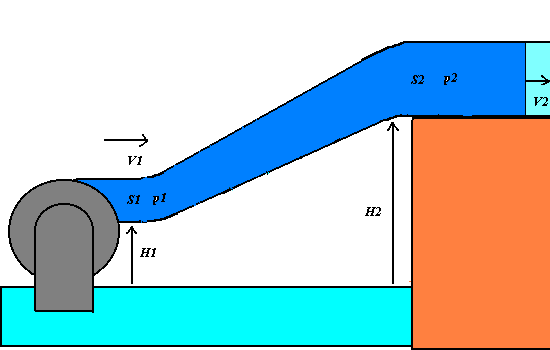
1) We apply the energy conservation principle to an incompressible and non-viscous
liquid having the density r, that flows across
an oblique varying-section pipe with the little section S1 at the level H1 and the great section at the level H2.
If p1 and p2 are the pressures of the
liquid respectively at S1
and S2, the work F1 d1 = p1 S1
d1, in relation to the displacement d1,is made by the
pressure force F1 = p1
S1,that is the force, directed to right, that the liquid on the left of S1 effects on the liquid going
into the pipe,whereas the work F2 d2 = p2S2d2,
in relation to the displacement d2,is
made by the pressure force F2 = p2 S2
that the liquid that goes out from the pipe effects against the liquid that on the right
of S2.
The application of the work-energy theorem to the volume of liquid S1
d1= S2d2 consists in equating the work
L = p2 S2 d2-p1 S1
d1 to the sum of both the increase of the gravitational potential
energy of the liquid mass m =rS2d1
= rS2 d2, that is given by
DU = r S2 d2 g
H2- r S1 d1 g H1
and the increase of the kinetic energy
DK= ( 1/2 ) r S2 d2 V22
- ( 1/2 )r S1 d1
V12 .
Then we get:
L = DU + DK.
By ordering opportunely the terms, we get:
p1 S1d1 + ( 1/2 ) r S1 d1 V12 + r S1 d1 g H1 =
p2 S2d2 + ( 1/2 ) r S2d2 V22 + r S2 d2 g H2 .
If we divide both members of the equation by S1 d1
=S2 d2 = v
(that is the volume of the liquid element we consider ),we get the Bernoulli theorem, that
is equivalent to the conservation principle of the total mechanical energy applied to a
liquid or a gas:
p1 + (1/2 )r V12
+ r g
H1 = p2 + (1/2 )r V22+ r g H2 = constant.
The Bernoulli theorem states that in any point of the varying-section pipe, the total
mechanical energy of an unitary liquid volume, that is given by the sum of the pressure p, the dynamic (or kinetic pressure)
(1/2)r V2(that is
equivalent to the kinetic energy per a unitary volume) and the hydrostatic pressure r g H (that is equivalent to the
gravitational potential energy per a unitary volume).
If we take in account that, in relation to the liquid mass
m = r S1d1 = r
S2 d2 passing across the pipe in the time Dt, the speed of the liquid,according to
the definition of the volumetric flux( Q = SV in m3/s ), varies with the inverse proportionality
law in relation to the section of the pipe (S1d1
= r S2 d2; S1V1Dt = S2 V2Dt ,we deduce that if, in particular, the pipe
is horizontal, the speed increases where the section diminishes and that therefore,because
the sum of the 3 pressures must be constant,in a narrowing pipe the pressure diminishes.
Viceversa, where the section increases, the speed diminishes and the pressure increases.
If r = 1000 kg/m3 (r is the density of water ),
V1= 25 m/s, S1=
100 cm2, H1 = 2 m,
p1 = 3 atmospheres = 3 x 1,013 x 105
N/m2 = 3, 039 x 105 N/m2,
S2 = 200 cm2, H2
= 5,2 m,
p2 = 5 atmospheres = 5 x 1,013 x 105
N/m2 = 5,065 x 105 N/m2,
the speed V2 assumes the value that is gotten from
the equation:
3,039 x 105 + 0,5 x 1000 x 625 + 1000 x 9,81 x 2 =
= 5, 065 x 105 + 0,5 x 1000 x V22
+ 1000 x 9, 81 x 5,2 ;
3, 039 x 105 + 0,5 x 1000 x 625 + 1000 x 9, 81 x 2- 5,065 x 105-1000
x 9, 81 x 5,2 = 0,5 x 1000 V22 ;
500 V22 = (3, 039 - 5,065) x
105 + 1000 x 9, 81 x ( 2-5,2) +
0,5 x 1000 x 625 = -202600-31392+ 312500 ~= 78508 .
V2 = square root of ( 78508/500 ) = square root of
157 ~= 12,5 m/s.
The volumetric flux is P = S1V1 = S2
V2 = 100 x 10-4 x 25m/s
~= 0.25 m3/s.
We observe that the speed V2 is equal to V1/2, since
S2 = 2 S1.
Both the increase of 2 atmospheres of the pressure p of the
liquid and the increase of the gravitational potential energy of the liquid, per a volume
unit, in relation to the level increasing of 3 m, are gotten to expenses of the diminution
of the kinetic energy of the liquid, per a volume unit, that is to expenses of the
diminution of the dynamic pressure (1/2 )r
V2.
1) If we stay in a car at rest on the road and another car is passing near us with high
speed, we feel a temporary side push that makes our car approach our to the moving car.
In fact, according to the Bernoulli theorem, the increase of the speed of the air in the
space between the cars,that behaves as the narrowing of a pipe, determines a pressure
diminution in comparison with the atmospheric pressure,which makes the cars approach each
other.
2) The wing of an airplane is subjected to an aerodynamic thrust upwards (the lift
capacity), that is as greater as greater is the difference between the pressure under the
wing and the one over it.
Since the greater is the pressure difference, the greater is the speed of the airplane, it
is deduced that the superior face of the wing behaves as the narrowing of a pipe, as it
may verified by studying the aerodynamic behaviour of a model of the wing in the wind
tunnel.
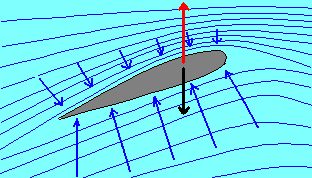
In particular,if the liquid is viscous,it is necessary to take account of the heat quantity generated per a unitary volume, because of the intern friction (viscosity) of the liquid.
From the enunciation of the energy conservation principle derives necessarily the first
principle of thermodynamics,that is nothing but a detail of the energy conservation
principle, applied to all the phenomena that implicate the transformation of some
mechanical,electric or magnetic work into heat, that is into thermal energy and,
viceversa, of heat into work, with the limitations imposed to the heat engines by the second principle of
thermodynamics.
The first principle of thermodynamics, because it is equivalent to the energy conservation
principle in relation to the thermal phenomena, states that it isn't possible to carry out
the so-called "perpetuum mobile" of the first type and that,
therefore,cannot be constructed a thermal engine producing some mechanical work without
absorbing any thermal energy.
1) The conversion into heat of the mechanical work produced by the friction forces, for
example the one that takes place in the brakes of a car or of a train.
2) The conversion into heat of the work made to drive a nail in a piece of wood or to fold
up more times a metallic pole;
3) The conversion into heat of the work made by an electric generator to maintain the
electric current in a resistor ( electric radiators,water heaters and electric cookers);
4) The conversion into heat of the work made to compress a gas.
1) Let's consider the heating of a gas at the constant pressure p
in a cylinder furnished with a piston having the section S,
which is able to move owing the constant force F.
If the force F is produced by the atmospheric pressure
together with another possible constant force acting on the piston, we have:
Q = L + DU, where Q is the heat absorbed by the gas,
L = F Dh = p S Dh = p DV is the work made by the gas
expanding against the constant pressure with the volume increase DV = S Dh ,
DU = U final-U initial is the
increase of the energy U inside the gas that is warming up.
The relation Q = L +DU expresses the first principle of thermodynamics.
2) The conversion into mechanical work of the heat quantity
Q = Qa-Qb, that, in the thermodynamic cycle of a thermal
engine,is given by the difference between the heat quantity Qa
that is furnished by a heat source at the higher temperature Ta
(this is the heat that is used to supply hot steam to a turbine, and is furnished as by
the combustion of the air-petrol or the air-oil mixture in a internal combustion engine,
as by the combustion of coal, natural gas or mineral oil, as by a nuclear fission
reactor), and the heat quantity Qb that is released by the
engine, at a lower temperature Tb, across the radiator (in a
car) or across the condenser, in the case of a thermal or nuclear power station.
The condenser requires some flowing sea or river water to cool the warm steam going out of
the turbine after the production of mechanical work.
The practical impossibility to transform into mechanical work the whole heat quantity Qa furnished by the thermal source at the higher temperature Ta, is stated by the second principle of thermodynamics, that was
formulated in XIX century in several, but equivalent,different ways, by Lord Kelvin
(William Thomson) and Rudolph Clausius
(a German physicist, 1822-1888 ),who are known as the pioneers of thermodynamics, together
with the French engineer Sadi Carnot
(1796-1832 ), who in 1824, by studying the energetic efficiency of the real thermal
engines, understood that their energetic efficiency
[ r = L/Qa = ( Qa-Qb )/Qa = ( Ta-Tb )/Ta = 1-Tb/Ta ] cannot ever
overcome the one of an ideal thermal engine (the so-called Carnot ideal thermal engine
),which is made to work between the same temperatures Ta and Tb, expressed in Kelvin degrees
( T °K = t °C + 273,16).
Lord Kelvin,by means of thermodynamic considerations, taking account that all the attempts
made to build a thermal engine that used an only heat source at a constant temperature,
enunciated the second principle of thermodynamics, affirming the impossibility to build
such a thermal engine.
The second principle of thermodynamics is a natural law that prevents to exploit
boundlessly and entirely the immense reserves of heat energy stored in the oceans and in
the subsoil ( the so-called "perpetuum mobile" of the second
kind),because is always inevitable to transfer a noticeable quantity of heat to the source
at smaller temperature,that is to the environment in which operates the thermal engine.
In other words, the second principle of thermodynamics states that to transform in a
continuous mode heat into mechanical work it is necessary to dispose of a temperature
difference and then of two thermal sources at different temperatures.
It may be showed that the Clausius formulation of the second principle of thermodynamics
is equivalent to the one of Lord Kelvin.
Clausius affirmed that it is impossible to build an ideal refrigerator, that is a
refrigerator that transfers heat from a body to another at a greater temperature, without
employing some mechanical work.
In an equivalent mode we can say that the second principle of thermodynamics states the
natural direction of the heat flux,from a body at a greater temperature to another at a
smaller temperature.
To reverse the natural flux of the heat it is always necessary to employ some mechanical
work.
The energetic efficiency r = L/Qa = (
Qa-Qb )/Qa of real thermal engines (as steam engines, internal combustion
engines,steam turbines) assumes, generally, the following practical values:
Petrol internal combustion engines ( based on the Otto thermodynamic cycle ): r = 25 % ;
Diesel engines: r = 32 % ;
Steam turbines (based on the Rankine thermodynamic cycle ):
r = 40 %.
These low values of the energetic efficiency implicate always, as it is already said, the
transfer of some heat to the environment, unless it is used to warm up rooms.
The heat energy wasted increases artificially the temperature of the air and of the
cooling water, with remarkable damages for the environment.
This negative phenomenon is responsible for the energy degradation principle, that affirms
that the heat energy at high temperature, because it cannot be transformed integrally into
mechanical work, as states the second principle of thermodynamics, implicates great wastes
of energy forms of higher quality (as the chemical or nuclear energy ) that, in the
thermodynamic conversion process used to get mechanical energy, are transforming into heat
energy at low temperature, that cannot any longer be reconverted integrally into higher
quality energy forms.
These phenomena, although the energy conservation principle is always valid, determines an
increasing energy unavailability, that can be understood by the classical example of two
tanks filled with water, provided the temperature difference between the tanks is suitable
to they can be used as thermal sources to make a thermal engine operate producing
mechanical energy.
If instead the two water masses are mixed till they reach thermal equilibrium, from it
results an only thermal source at an intermediate temperature in comparison with the
initial ones, without violating the energy conservation principle, since the heat acquired
by the cool water mass is equal to the heat lost by the hot water mass.
Therefore it isn't possible any longer to use the only water mass of water at a uniform
temperature to make the thermal engine operate.
This example shows that in the heat propagation from the warm water to the cool one there
is an irreversible process that increases the disorder of the system.
The increase of the disorder of a thermodynamic system is measured by a very important
thermodynamic quantity: the entropy.
In the universe, characterized by irreversible thermodynamic phenomena as the propagation
of the heat from a warm body to a cool one, the entropy increases always, whereas the
total energy preserves in all its forms.
Therefore, the second principle of the thermodynamics can be enunciated also, following
Clausius, as the principle of the entropy increasing .
When we start the engine of a car, even if the entropy of the thermal engine doesn't
change, because it operates by means of a real thermodynamic cycle, that goes across any
irreversible transformations ( expansions and compressions ) that make the engine come
back into the initial state, instead the entropy of the environment and the one of the
universe, increase always.
If it is thought to build an ideal thermal engine (the Carnot thermal engine ) with an
energetic efficiency r=100 %, that is
r= (Qa-Qb )/Qa = ( Ta-Tb ) /Ta = 1-Tb/Ta
= 1 for Tb = 0, then it would be necessary to cool the
condenser of the car at the absolute zero temperature ( Tb = 0 °K).
Apart from the greatest practical difficulties that one would meet to realize such a car,
it is necessary take in account that it is impossible to achieve this aim,beacuse of
(the Nernst's principle), that states that, the more one approaches to the absolute
zero ( t =-273 °C, corresponding to T
= 0 °K),even of some millionths of a Kelvin degree, even more it is difficult to
reduce the temperature.
In other words, it isn't possible to reach the temperature of the absolute zero with a
finite number of transformations.
The third principle is connected directly to the behaviour of matter at the absolute
zero,because the Heisenberg uncertainty principle makes it impossible to locate exactly an
elementary particle, whose linear momentum is known exactly.
Therefore to all the quantum states at the zero point, a non-zero least energy is
associated, the so-called zero-point energy.
It is said, alternatively, that at the zero point all the states have the same entropy.